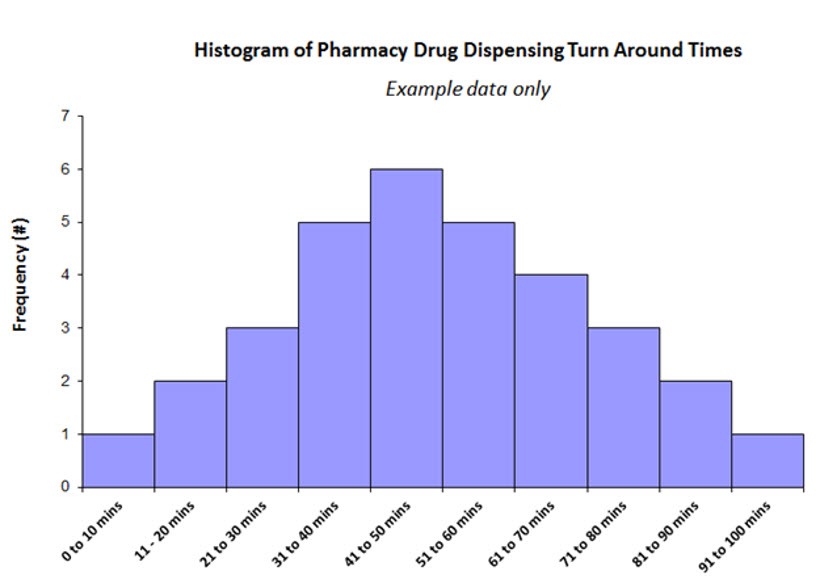
Histograms are like bar charts; they are an approach to show counts of information. A bar graph charts counts against categories; the height of the bar shows the quantity of things in that classification. A histogram shows the same unmitigated factors in “bins”.
When you make a histogram, you are making a bar diagram that shows what number of data focuses are inside a range (an interval), it is called a bin. Typically, you pick the range that best fits your data. There are no set principles about what number of bins you can have, yet the rule of thumbs says that you can have 5-20 bins. Any in excess of 20 bins and your diagram will be difficult to read. Less than 5 bins and your chart will have close to nothing (assuming any) which means. Most charts you’ll make in basic statistics will have around 5 to 20 bins.
Unlike bar graph, the area of a bar in a histogram represents frequency, not the height. The frequency is calculated by multiplying the width of bin by height. The height of a bar in a histogram shows frequency (counts) just if the bin widths are equally separated. For instance, If you are plotting extents of earthquakes and your bins are 3-5, 5-7 and 7-9, each bin is spaced two numbers separated thus the height of the bar would equal with the frequency. Be that as it may, histograms don’t generally have even bins. At the point when a histogram has uneven bins, the height does not equivalent the frequency.
How to Draw a Histogram
A histogram is a method for diagramming groups of numbers as per how they show up. This article will demonstrate to you how to draw a histogram by hand, yet you can also draw one by using the technology, such as making an Excel histogram. Picking bins in statistics is typically a matter of an informed guess. When you make a histogram by hand, you’re normally stuck with the bin settings. With Excel (or other programming), you can change the bins after you’ve made the histogram, enabling you to play around with bin sizes until the point that you have a graph you’re content with. Once in a while you may need to make a histogram by hand, particularly in case you’re making a relative frequency histogram; Technology like TI-83s will just make normal frequency histograms. On the off chance that you need to draw a histogram by hand, here’s the easy way.
Drawing a Histogram
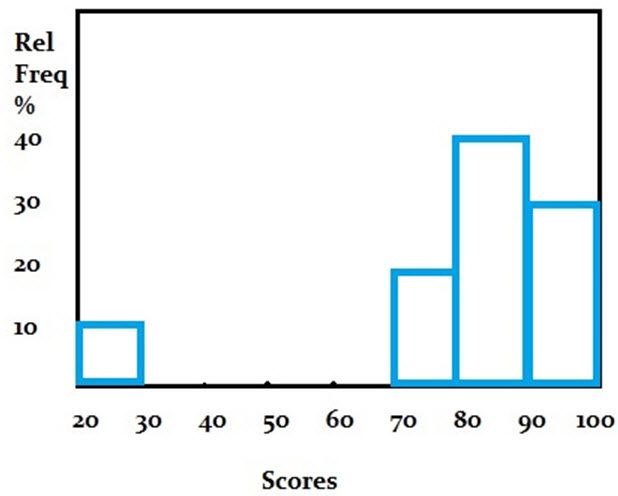
Sample: Draw a histogram for the following test scores: 99, 97, 94, 88, 84, 81, 80, 77, 71, and 25.
First Step: Draw and label your x and y axis
For the above examples, the x-axis would be named as scores whereas the y-axis would be named as ‘Relative frequency percentage’
Second step: Choose the number of bins
Choose the number of bins and label your diagram, for this example, groups of 10 (the x-axis are the bins) are a decent decision (it would seem that you’ll have 5 bars of maybe one or two items in the group).
Third step: Divide 100 by the number of data points
Divide 100 by the number of data points to get the idea of where to put your frequency “ticks”. We have 10 things in our data set, so it makes the most of sense to count by 100/10 = 10% (one thing would equal with 10% of the total value).
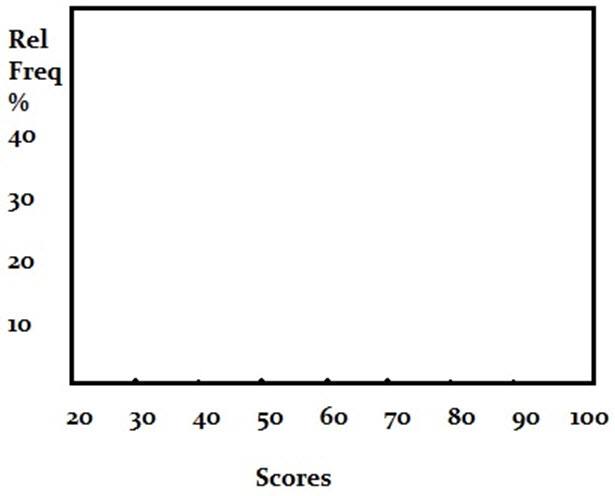
Fourth Step: Count how many items are in each bin and then sketch a rectangle on the graph
Count the items in each bin and afterward outline a rectangle on the diagram that relates to the percentage of the total that bins fills. In this example data set, the main bin (20-30) has 1 score; 70-80 has two scores. If a thing falls on a bin limit (i.e. 80), put it in the following bin up (80 would go in 80-90). At the end your histogram would end up liking like this.
When to Use Histograms
Histograms like this are often used in day to day work when analyzing data or for example when determining the capability of a process.